
update 2020.05.10

2016.12.15 processページを更新
『Tambatitanis amicitiae の復元プロセス1(頭骨編)』をアップしました。
2015.09.14 galleryページを更新
nature artに鳥類系統樹マンダラの原画をまとめてアップしました。現在、ジュンク堂池袋本店7F理工コーナーで、ポスター販売と...
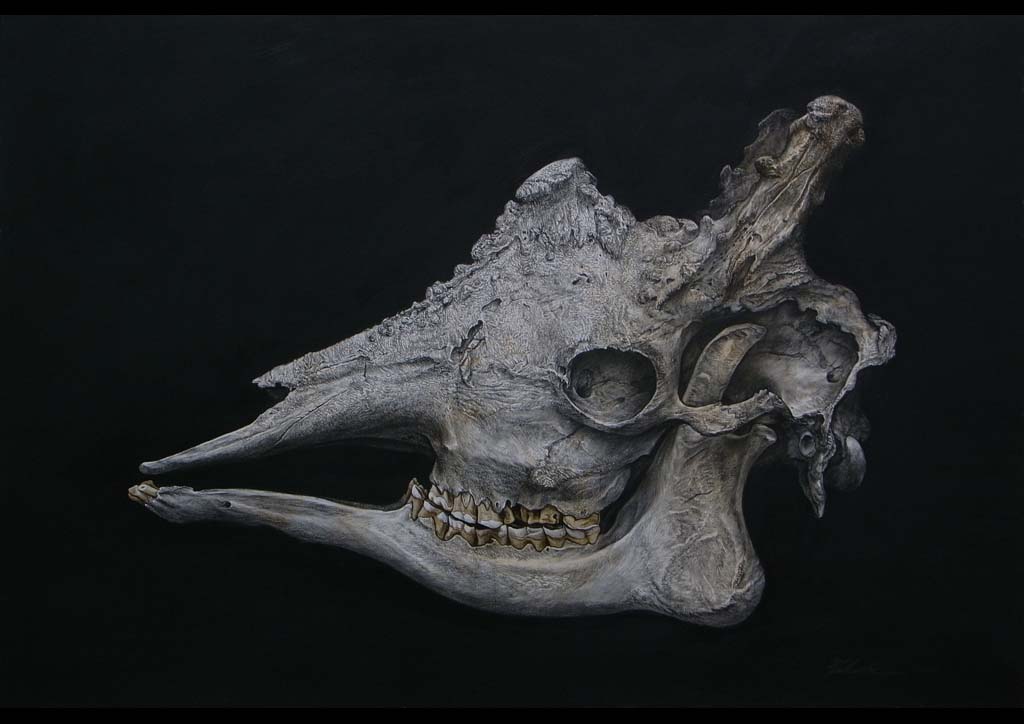
2015.09.14 top画像を更新
top画像を『Giraffe skull』に更新しました。
2015.06.11 galleryページを更新
nature artに鳥類系統樹マンダラの原画をまとめてアップしました。
2015.06.08 galleryページを更新
『女性ヌードクロッキー』をアップ。
2015.05.27 galleryページを更新
『女性ヌードドローイング』『男性ヌードドローイング』をアップ。
2015.05.08 processページを更新
「『アケボノゾウの群れ』制作プロセス2」をアップ。
2015.05.07 processページを更新
「『アケボノゾウの群れ』制作プロセス1」をアップ